Fonction à variation bornée

En analyse, une fonction est dite à variation bornée quand elle vérifie une certaine condition de régularité. Cette condition a été introduite en 1881 par le mathématicien Camille Jordan pour étendre le théorème de Dirichlet sur la convergence des séries de Fourier.

Définition

Soit f une fonction définie sur un ensemble totalement ordonné T et à valeurs dans un espace métrique (E, d).

Pour toute subdivision σ = (x₀, x₁, … , x_n) d'un intervalle quelconque de T, on définit V(f, σ) par :

V(f,\sigma )=\sum _{i=1}^{n}d(f(x_{i-1}),f(x_{i})).

On appelle variation totale de f sur T la valeur V_T(f) ∈ ℝ définie par :

V_{T}(f)=\sup _{\sigma }V(f,\sigma ).

On dit que f est à variation bornée si cette borne supérieure V_T(f) est finie, autrement dit si l'« arc » (non nécessairement continu) défini par f est rectifiable au sens de Jordan.

Intérêt de la notion

Les fonctions monotones forment une classe importante de fonctions en analyse. Cependant elle présente l'inconvénient de ne pas être invariante pour des opérations algébriques basiques : la somme de deux fonctions monotones par exemple n'est pas nécessairement monotone. Comme toute fonction à variations bornées est somme de deux fonctions monotones et réciproquement, les fonctions à variations bornées peuvent être vues comme une généralisation des fonctions monotones mais avec l'avantage que l'ensemble des fonctions à variations bornées muni de l'addition ou de la multiplication forme un anneau : la somme et le produit de deux fonctions à variations bornées est à variations bornées.

Propriétés

La variation totale (finie ou infinie) d'une fonction f continue sur un segment réel [a, b] est non seulement la borne supérieure des V(f, σ) quand σ parcourt les subdivisions de [a, b], mais aussi leur limite, quand le pas de la subdivision σ tend vers 0. On en déduit que pour une fonction continue à variation bornée f, l'application t ↦ V_{[a, t]}(f) est continue.
Si φ est une bijection croissante d'un autre ensemble totalement ordonné S vers T, la variation totale de f∘φ sur S est égale à celle de f sur T.
Pour tout espace vectoriel normé E, les fonctions à variation bornée forment un sous-espace vectoriel de l'espace des fonctions de T dans E.
Toute fonction F absolument continue (en particulier toute fonction lipschitzienne) est à variation bornée. Autrement dit : si f est intégrable au sens de Lebesgue sur un intervalle I alors, pour a fixé dans I, la fonction $x\mapsto F(x)=\int _{a}^{x}f(t)~\mathrm {d} t$ est à variation bornée. En effet, $V_{a}^{x}(F)\leq \int _{a}^{x}\vert f(t)\vert dt\leq \int _{I}\vert f(t)\vert ~\mathrm {d} t.$
Toute fonction à variation bornée est réglée (c'est-à-dire limite uniforme d'une suite de fonctions en escalier).
Les fonctions à variation bornée d'un segment réel dans ℝ sont exactement les différences de deux fonctions croissantes (une telle décomposition f = g – h est loin d'être unique ; si f est continue, g et h peuvent être choisies continues : par exemple h(t) = V_{[a, t]}(f) et g = f h). On en déduit que leurs discontinuités sont inessentielles et forment un ensemble au plus dénombrable et que ces fonctions sont dérivables presque partout (au sens de la mesure de Lebesgue), de dérivées localement intégrables.
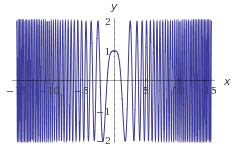
Il existe des fonctions dérivables à variation totale infinie, comme la fonction f définie sur [–1, 1] par f(x) = x²cos²(π/x²) si x ≠ 0 et f(0) = 0.

Généralisation aux fonctions à variables multiples

Une définition étendue aux fonctions à variables multiples peut se faire par la variation de Vitali^,. Proposée par Vitali, elle a été reprise par Lebesgue et Fréchet.

Soit une fonction f définie sur un pavé $[a_{1},b_{1}]\times \cdots \times [a_{n},b_{n}]\subseteq \mathbb {R} ^{n}$ . On note :

\Delta _{h_{k}}(f,x)=f(x_{1},x_{2},\cdots ,x_{k} h_{k},\cdots ,x_{n})-f(x_{1},x_{2},\cdots ,x_{k},\cdots ,x_{n})

puis, de façon récursive,

\Delta _{h_{1},h_{2},\cdots ,h_{k}}(f,x)=\Delta _{h_{k}}(\Delta _{h_{1},h_{2},\cdots ,h_{k-1}},x).

On se donne ensuite des suites de points $\pi _{k}$ sur chaque direction $a_{k}=t_{k}^{1$ , et on associe $h_{k}^{i}=t_{k}^{i 1}-t_{k}^{i}.$

La variation au sens de Vitali de f est donnée par :

$V^{n}(f)=\sup _{(\pi _{1},...\pi _{n})}\sum _{k=1}^{n}\sum _{i_{k}=1}^{N_{k}}\left|\Delta _{h_{1}^{i_{1}},h_{2}^{i_{2}},\cdots ,h_{k}^{i_{k}}}\left(f,(x_{1}^{i_{1}},x_{2}^{i_{2}},\cdots ,x_{k}^{i_{k}})\right)\right|$

Cette définition de la variation peut être étendue à travers la définition de la variation de Hardy-Krause :

La variation de Hardy-Krause de f est donnée par :

$V(f)=\sum V^{n}(f)$
où la somme est faite sur toutes les faces de tous les sous-intervalles du pavé $[a_{1},b_{1}]\times \cdots \times [a_{n},b_{n}]\subseteq \mathbb {R} ^{n}$ de dimension inférieure ou égale à n.